diff与patch算法
Vue2与Vue3 diff概括
在Vue2中,diff算法可以归结为:
- 头和头比
- 尾和尾比
- 头和尾比
- 尾和头比
- 都没有命中的对比
而在Vue3中,diff算法被优化为:
- 头和头比
- 尾和尾比
- 基于最长递增子序列进行移动/添加/删除
解读
1. 从头比对
首先,对新旧节点c1, c2,定义了以下几个指针:
i=0,该指针指向头部的标记位e1 = c1.length - 1,该指针指向c1的尾部l2 = c2.length; e2 = l2 -1,该指针指向c2的尾部
const patchKeyedChildren = (c1, c2, container, parentAnchor, parentComponent, parentSuspense, isSVG, optimized) => {
let i = 0;
const l2 = c2.length;
let e1 = c1.length - 1;
let e2 = l2 - 1;
// 从头开始比对
while(i<=e1 && i<=e2) {
const n1 = c1[i];
const n2 = c2[i]; // 这里简化了一些内容
if (isSameVNodeType(n1, n2)) {
patch(n1, n2, container, parentAnchor, parentComponent, parentSuspense, isSVG, optimized); // 如果是sameVNode则递归patch
} else {
break;
}
i++;
}
}2. 从尾比对
const patchKeyedChildren = (c1, c2, container, parentAnchor, parentComponent, parentSuspense, isSVG, optimized) => {
let i = 0;
const l2 = c2.length;
let e1 = c1.length - 1;
let e2 = l2 - 1;
// 从头开始比对
// ...
//
// 尾比对
while(i<=e1 && i<=e2) {
const n1 = c1[e1];
const n2 = c2[e2]; // 简化了一些内容
if (isSameVNodeType(n1, n2)) {
patch(n1, n2, container, parentAnchor, parentComponent, parentSuspense, isSVG, optimized); // 如果是sameVNode则递归patch
} else {
break;
}
e1--;
e2--;
}
}3. 在上面基础上实现新增/删除节点
(1) 新增节点
<!-- c1 -->
<ul>
<li key="a">a</li>
<li key="a">b</li>
<li key="a">c</li>
<li key="a">d</li>
</ul>
<!-- c2 -->
<ul>
<li key="a">a</li>
<li key="a">b</li>
<li key="a">e</li>
<li key="a">c</li>
<li key="a">d</li>
</ul>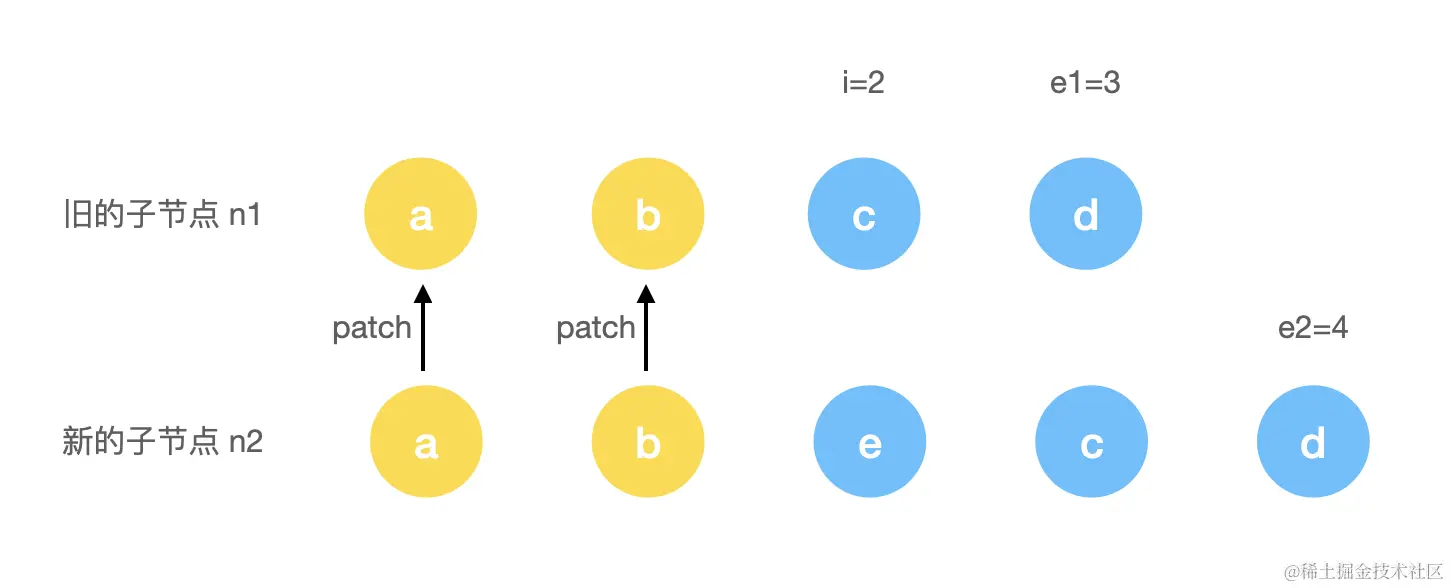
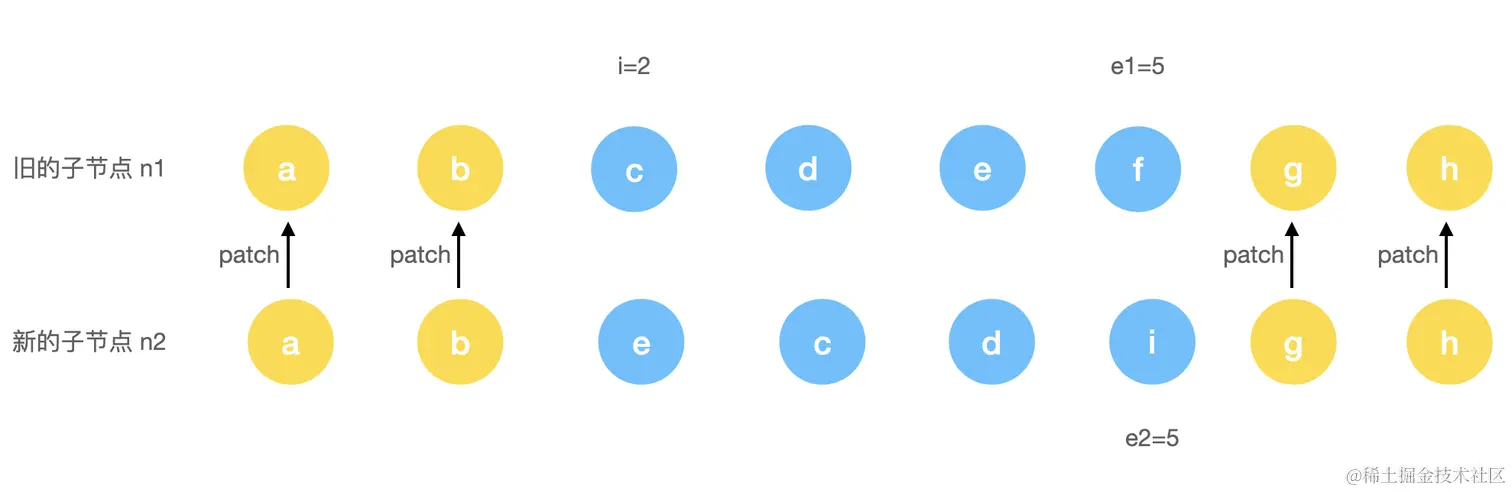
第一步执行完,此时会对a, b两个进行patch。当i=2的时候,由于此时两个节点不一致,所以进入到尾部对比流程。
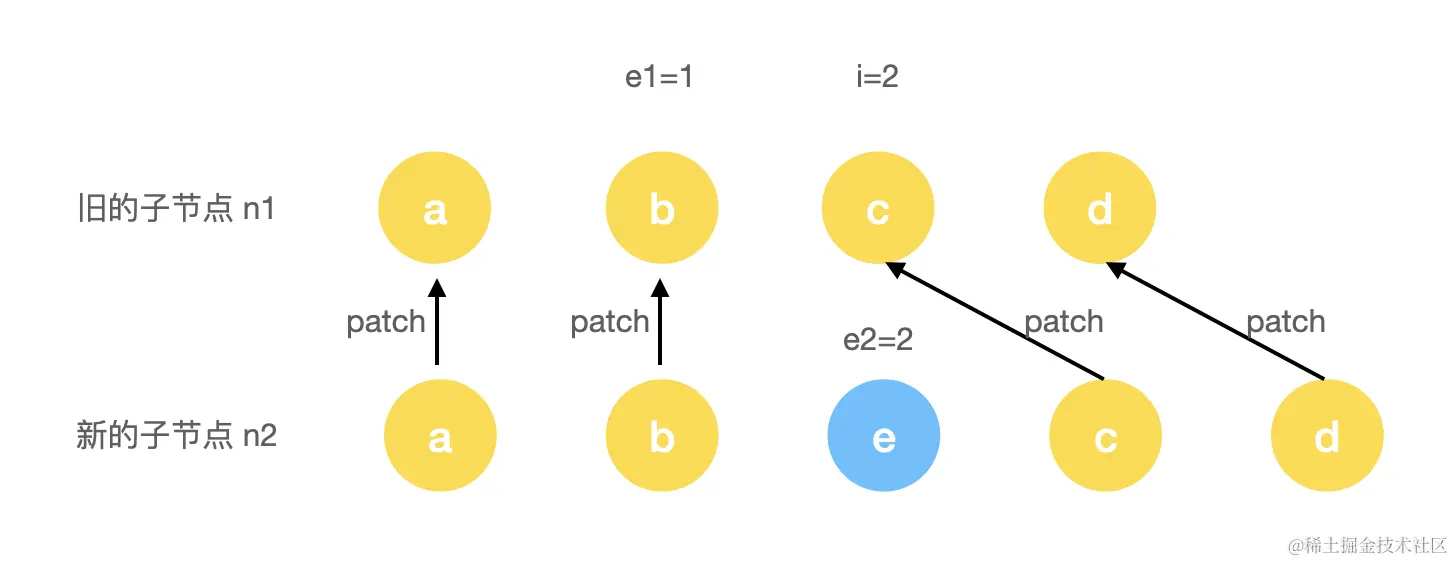
当前执行完后,会完成c, d两个节点的patch操作,此时由于e1<i,因此尾对比流程结束了,发现多了一个key=e的新节点,因此我们需要进行新增节点操作。
const patchKeyedChildren = (c1, c2, container, parentAnchor, parentComponent, parentSuspense, isSVG, optimized) => {
let i = 0;
const l2 = c2.length;
let e1 = c1.length - 1;
let e2 = l2 - 1;
// 从头开始比对
// ...
// 尾比对
// ...
// 新增节点操作
if (i>e1) {
if(i<=e2) {
const nextPos = e2 + 1;
const anchor = nextPos < l2 ? c2[nextPos].el : parentAnchor;
while(i<=e2) {
patch(null, c2[i], anchor, parentComponent, parentSuspense, isSVG); // patch新增节点
i++;
}
}
}
}(2)删除节点
<!-- c1 -->
<ul>
<li key="a">a</li>
<li key="a">b</li>
<li key="a">e</li>
<li key="a">c</li>
<li key="a">d</li>
</ul>
<!-- c2 -->
<ul>
<li key="a">a</li>
<li key="a">b</li>
<li key="a">c</li>
<li key="a">d</li>
</ul>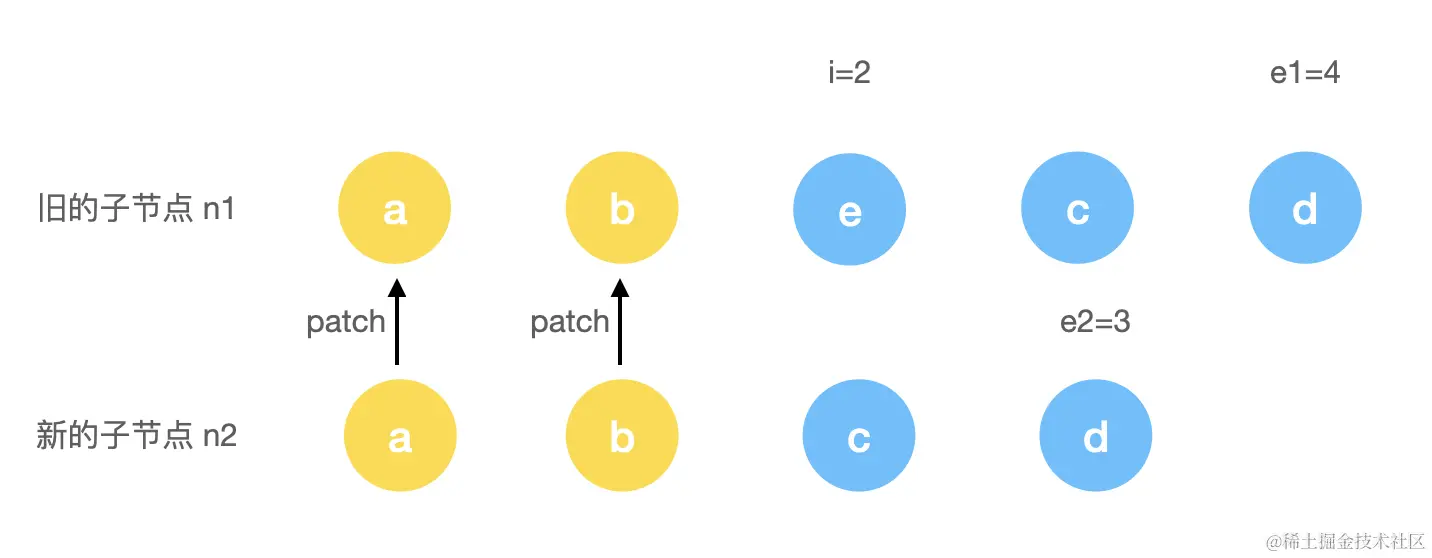
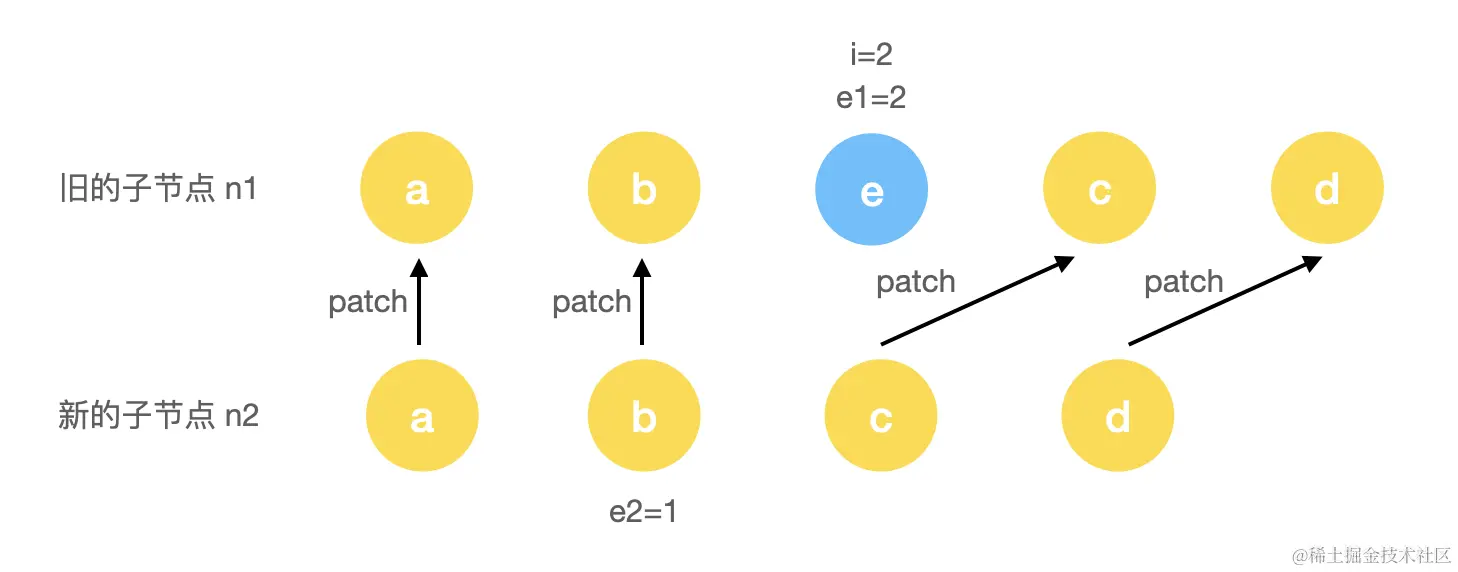
事实上与新增节点操作类似,只是由c2多变成了c1多
const patchKeyedChildren = (c1, c2, container, parentAnchor, parentComponent, parentSuspense, isSVG, optimized) => {
let i = 0;
const l2 = c2.length;
let e1 = c1.length - 1;
let e2 = l2 - 1;
// 从头开始比对
// ...
// 尾比对
// ...
// 新增节点操作
// ...
// 删除节点操作
else if (i>e2) {
while (i<=e1) {
unmount(c1[i], parentComponent, parentSuspense, true);
i++;
}
}
}如果二者都不满足呢?(源码里面叫Unknown Squence)
这种情况下,i<e1&&i<e2。
一个前提
DOM更新的时候,性能优劣关系大致如下:属性更新 > 位置移动 > 增删节点。所以,我们尽量复用老节点,作属性更新操作,减少移动次数和增删节点次数。即尽量使用patch更新,实在不行再使用move移动节点
Vue的实现
1. 新旧位置找相同直接patch
(1) build key:index map for newChildren
即:构建新序列的key:index哈希表,用于旧节点搜索新位置。
const patchKeyedChildren(...args) {
// ...
else {
const keyToNewIndexMap = new Map();
for(let i=s2;i<=e2;i++) {
const newChild = c2[i]; // 省略一个optimize
if(newChild != null) {
keyToNewIndexMap.set(newChild, i);
}
}
}
}(2) 查找旧节点在新节点的位置
- 如果旧节点不在新节点中,即
keyToNewIndexMap中找不到对应的index,则unmount这个旧节点 - 否则,
patch这两个对应的节点 - 如果旧节点访问完成还有新的剩余,则
patch(null, nextChild, container...),新增这个新节点 - 如果遍历过程中需要移动,则寻找最长公共递增子序列,进行最小位置移动。
else {
// ... KeyToNewIndexMap
let patched = 0; // 已经更新的节点数
let toBePatched = e2 - s2 + 1; // 需要进行更新的节点数
let moved = false; // 标记是否需要节点移动
let maxNewIndexSoFar = 0; // 标记是否有节点进行了位置移动'
// works as Map<newIndex, oldIndex>
// Note that oldIndex is offset by +1
// and oldIndex = 0 is a special value indicating the new node has
// no corresponding old node.
// used for determining longest stable subsequence
const newIndexToOldIndexMap = new Array(toBePatched).fill(0); // 记录新节点在旧节点的位置数组,并填满0,这里源码用了for遍历优化一些性能吧
// 开始遍历旧节点查新位置
for(let i=s1;i<=e1;i++){
const prevChild = c1[i];
// 所有新节点已经patched了,所以剩下的需要删除
if(pathed>=toBePatched) {
unmount(prevChild, parentComponent, parentSuspense, true);
continue;
}
let newIndex;
if(prevChild.key != null) {
newIndex = = keyToNewIndexMap.get(prevChild); // 旧节点的新位置
} else {
// 如果没有key(key-less node),只能找新节点中相同类型且没有key的节点
for(j=s2;j<=e2;j++) {
if(
newIndexToOldIndexMap[j-s2] === 0 &&
isSameVNodeType(prevChild, c2[j])
) {
newIndex = j;
break;
}
}
}
if(newIndex === undefined) {
unmount(prevChild, parentComponent, parentSuspense, true); // 找不到
break;
} else {
newIndexToOldIndexMap[newIndex-s2] = i+1; // work as Map<newIndex, oldIndex>, oldIndex is offset by +1,主要是为了避免i为0的特殊情况
if (newIndex>=maxNewIndexSoFar) {
// 如果没有移动,那么index一定是增序的,否则一定有移动过
maxNewIndexSoFar = newIndex;
} else {
moved = true;
}
// patch新旧相同key节点
patch(prevChild, c2[newIndex], container, null, parentComponent, parentSuspense, isSVG, optimize);
patched++;
}
}
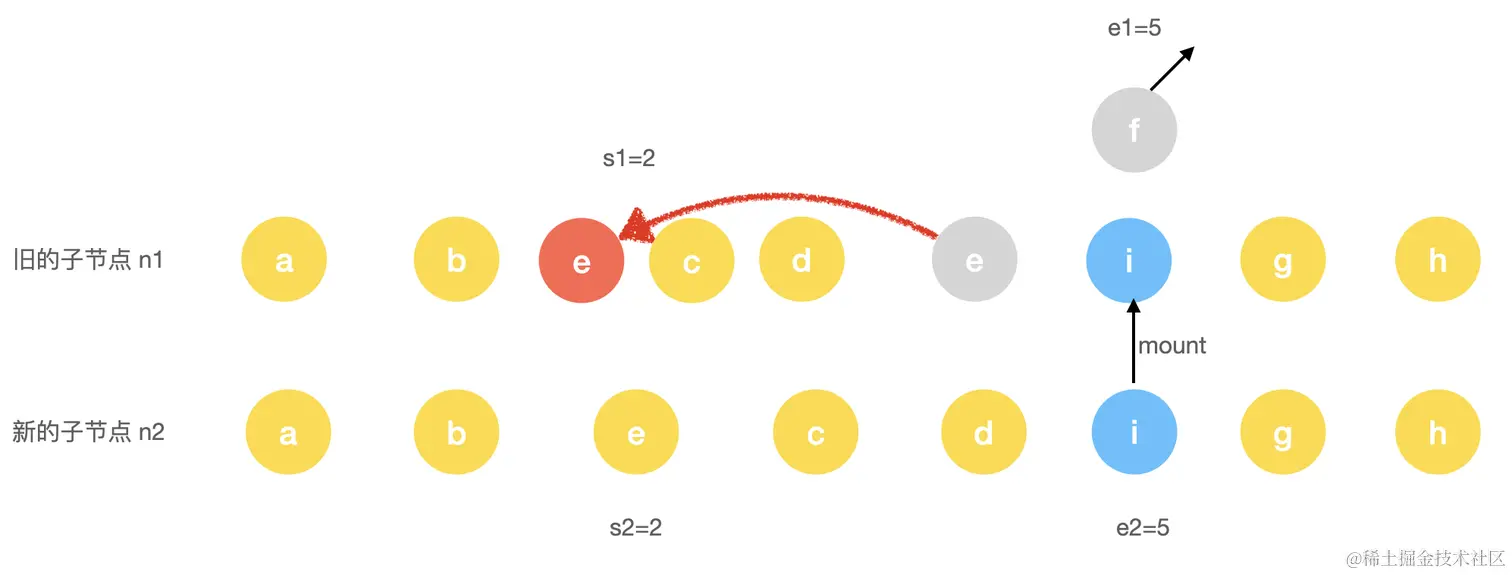
}直至这一步,我们对相同key的节点进行了patch操作,并且删除了一部分多余的旧节点。 不仅如此,我们还获得了newIndexToOldIndexMap与moved这两个变量,用于后续的最长公共递增序列算法的实现。
(3) 移动和新增节点
const increasingNewIndexSequence = moved
? getSequence(newIndexToOldIndexMap)
: EMPTY_ARRAY; // 空数组或求最长公共递增子序列(存的是Index而不是Key)
j = increasingNewIndexSequence.length - 1; //最长公共子序列尾索引
for(i=toBePatched - 1; i>=0; i--) {
// 反过来遍历,我们可以利用最后patch的节点作为anchor
const newIndex = s2 + i;
const newChild = c2[newIndex];
const anchor = newIndex + 1 < l2 ? c2[newIndex+1].el : parentAnchor; // l2 = c2.length;
if(newIndexToOldIndexMap[i] === 0) {
// 没有新到旧的映射,说明是新节点
patch(null, newChild, container, anchor, parentComponent, parentSuspense, isSVG, optimize);
} else if(moved) {
// 如果需要移动且
// 没有最长递增子序列
// 当前的节点不在最长递增子序列中
if (j<0 || i!==increasingNewIndexSequence[j]) {
// 如果当前的index不在递增子序列中,则把当前index的节点移动到上一个更新的节点前
move(nextChild, container, anchor, MoveType.REORDER);
} else {
// 否则,移动最长子序列的尾部指针
j--;
}
}
}因为,没有出现在递增子序列内的节点代表他们的位置被前移了,所以把这些节点前移即可。
附加内容:
1. GetSequence算法的实现
2. 为什么不建议使用index作为VNode.key
我们现在知道了,整个diff算法其实都是依赖于vNode.key来判断节点是否为同一个的,即key应该是VNode的唯一标识符,但是如果我们使用index作为标识符的话。
举个例子:
let c1 = [
{
id: 'a',
value: 'a'
},
{
id: 'b',
value: 'b'
},
{
id: 'c',
value: 'c'
}
];
let c2 = [
{
id: 'd',
value: 'd'
},
{
id: 'a',
value: 'a'
},
{
id: 'b',
value: 'b'
},
{
id: 'c',
value: 'c'
}
]此时我们发现,如果我们使用id作为key的话,在尾遍历后,只需要添加一个新节点即可完成patch,但是如果我们使用index的话,就会发现,我们需要从头到尾patch三个节点!再新增一个新的节点,这个相比使用id进行增删数组操作的损耗是非常非常大的!
因此,当我们使用到数组进行增删操作的时候,尽量避免使用index作为VNode.key
